Goodness of Fit
goodness of fit tests are used to test whether the counts of observations belonging to two or more categories differ from those under an expected model. For example, what is the likelihood of a sample of 60 women and 40 men in a class coming from a population where the sex ratio is actually 1:1? In this example, there is a single categorical variable of sex, with two categories of male and female.
The test statistic is:
where O and E are the observed and expected numbers in each of the categories from 1 to k.
The observed numbers come from your actual observations, in this example 60 and 40.The expected numbers are from a theoretical expectation of the frequencies under the model being tested. In this example, if you were testing against an expectation of a male:female ratio of 1:1, then you would expect 50 women and 50 men in a sample of 100 people.
For this example,
Running the analysis
You can calculate pretty easily with a calculator. You would then need to determine the probability of obtaining that value from the known probability distribution of .
pchisq(x, df, lower.tail = FALSE)with x = your value of , and degrees of freedom (df) = number of categories-1. The lower.tail = FALSE bit gives you the probability that is greater than your value.
Alternatively, you can do all of this in one go with the chisq.test function.
chisq.test(x, p)where x = the observed data (i.e., counts in each category) and p are the expected probabilities for each category.
In this example we would use:
chisq.test(x = c(60, 40), p = c(0.5, 0.5))where x is the observed range of numbers and p has the expected probabilities.
Note that it is very important that you use the actual counts as your observed data, not their proportions (i.e., 60 and 40, not 0.6 and 0.4). This makes sense if you understand that a sex ratio of 6:4 in a sample of 10 people is more likely to occur by chance when sampling from an equal sex ratio than a ratio of 600:400 in a sample of 1000 people.
You are not constrained to just two categories, or an expectation that the counts in each are equal. For example, to test whether the counts 10, 20 and 70 in three categories came from a population with expected frequencies of 0.25, 0.25 and 0.5, you would use:
chisq.test(x = c(10, 20, 70), p = c(0.25, 0.25, 0.5))Interpreting the results
The output from a goodness of fit test is very simple: the value of , the degrees of freedom (number of categories - 1) and the p-value. The p-value gives the likelihood of your observed counts coming from a population with the expected frequencies that you specified.
##
## Chi-squared test for given probabilities
##
## data: c(60, 40)
## X-squared = 4, df = 1, p-value = 0.0455In the sex ratio example, you should have obtained a p-value of 0.0455, which tells us that it is unlikely to obtain a sample of 60 women and 40 men from a population with an equal sex ratio. We would then conclude that they were likely to be sampled from a population that did not have an equal sex ratio.
To explore which of the categories had more observations than expected, or had fewer observations than expected, look at the standardised residuals.
chisq.test(x = c(60, 40), p = c(0.5, 0.5))$residualsThese are the differences between the observed and expected, standardised by the square root of the expected. These are standardised because any contrast of the absolute differences (observed - expected) can be misleading when the size of the expected values vary. For example, a difference of 5 from an expectation of 10 is an increase of 50%, but a difference of 5 from an expectation of 100 is only a 5% change.
Exploring the residuals becomes important when there are more than two categories in the test, as the test will only tell you if the observed frequencies differ from the expected across all categories, not which particular category is over- or under-represented.
Assumptions to check
Independence. The test assumes that the observations are classfied into each category independently of each other. This is a sampling design issue and is usually avoided by random sampling. In the sex ratio example, there would be problems is you deliberately chose women to add to your sample if you thought that you had enough men already.
Sample size. The statistic can only be reliably compared to the distribution if sample sizes are sufficiently large. You should check that at least 20% of the expected frequencies are larger than 5. You can see the expected counts for each category by adding $expected to the end of your test. For example,
chisq.test(x = c(60, 40), p = c(0.5, 0.5))$expectedIf this assumption has not been met, you could combine categories (if you have more than two), run a randomisation test or consider log-linear modelling.
Communicating the results
Written. The results of a goodness of fit test can be easily presented in the text of a results section. For example, “The sex ratio of the class of 100 students differed significantly from a 1:1 ratio (” = 4, df = 1, P = 0.0455).”
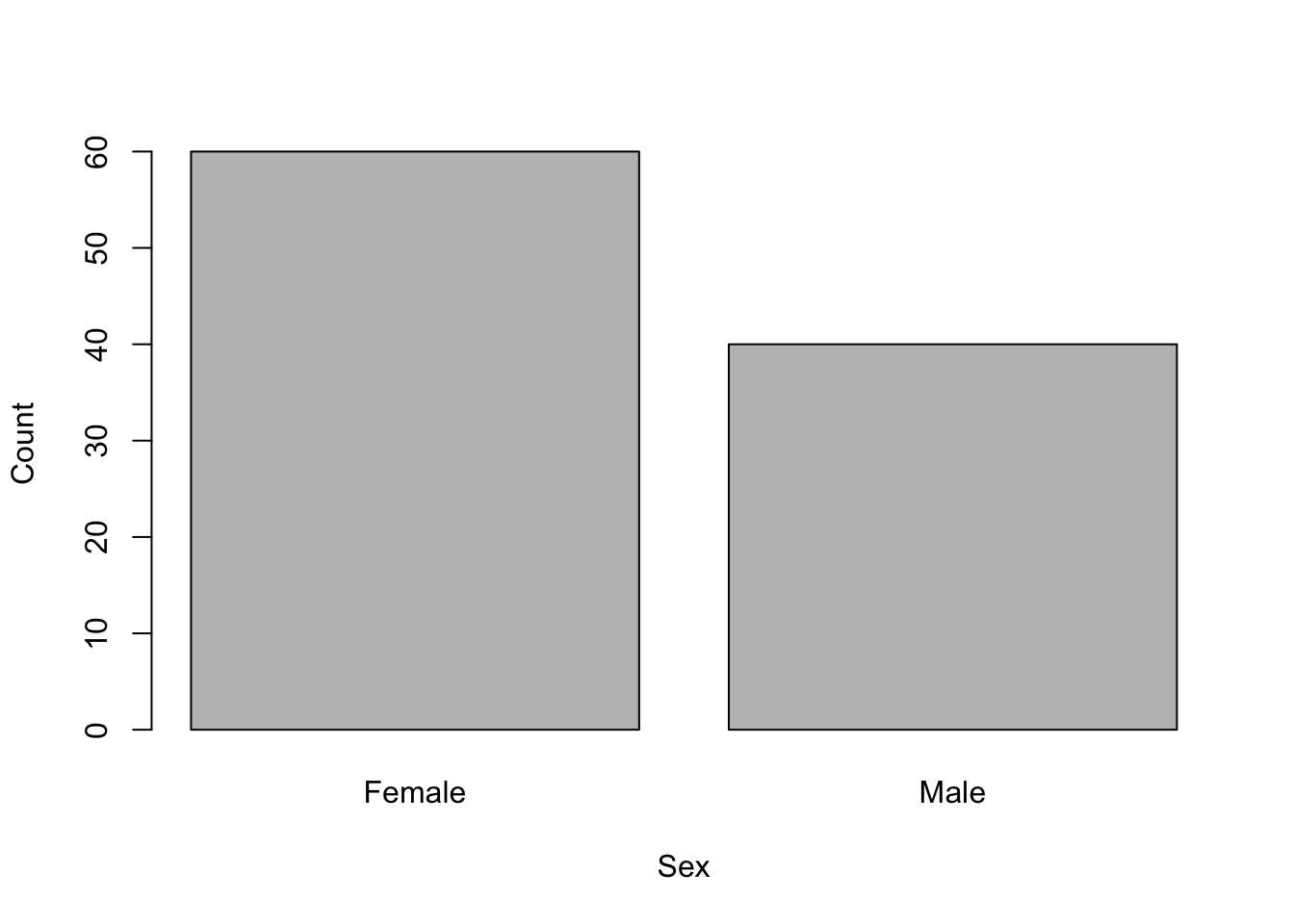
Visual. Count data are best presented as a bar plot with the counts on the Y axis and the categories on the X axis
barplot(c(60, 40), xlab = "Sex", ylab = "Count", names = c("Female", "Male"))See the graphing modules for making better versions of these figures that are suitable for reports or publications.
Further help
Type ?chisq.test to get the R help for this function.
Quinn and Keough (2002) Experimental design and data analysis for biologists. Cambridge University Press. Chapter 14. Analyzing frequencies.
McKillup (2012) Statistics explained. An introductory guide for life scientists. Cambridge University Press. Chapter 20.2 Comparing observed and expected frequencies: the chi-square test for goodness of fit.
Author: Alistair Poore
Year: 2016
Last updated: Feb 2022